时光如流，岁月不居，又到一年的毕业季，要说此时同学们表达情感最为直接与普遍的方式、那便是歌曲了。难以忘记“音浪太强”的夜晚，“稻香”的旋律伴着“还记得你说家是唯一的城堡”，激起近万人的共情……
   词作者笔下惊风雨、曲作者手中蕴雷暴，让我们得以惊叹词文那的含义、曲调那旋律；我若说“数学中的符号更甚音符，每一个都经历了更为漫长的发展，其乐音袅袅更值惊叹”，你或许会不得其解甚至不以为然。那就跟着……一起去探寻数学符号背后的“起源与发音”吧。
   远景学院始终奉行“每一堂课，就是一次学生的生命运动。只要学生足够投入，通过师生之间有温度的讨论，就可以训练自己的公众表达与批判思维能力。鉴于“在做中学”

的培养理念，同时期待学生能在课堂上获得更多实用性的知识，丰富数学课堂的形式，提高学生的学习兴趣。刘铭丽老师组织学生开展以“数学符号起源与发音”为主题的课堂展示活动，线上为同学们提供各种资料搜寻渠道，要求学生课下分组搜寻资料，整理并制作PPT，以课堂陈述方式展示。希望学生籍此感受到数学符号厚重的科学积淀、精妙的人文魅力，引导学生感悟数学文化，激起同学们学习数学知识的兴趣和应用数学思维的能力。
    接下来让我们一起看看学生调研结果：

第一篇：数学符号来源

1.  根号“√￣”的由来

十七世纪，法国数学家笛卡尔（1596-1650年）第一个使用了现今用的根号“√￣”。但是它的出现经历了一个漫长的过程，由“·”到“√”再到“√￣”

古时候，埃及人用记号“┌”表示平方根。

印度人在开平方时，在被开方数的前面写上ka。

1840年前后，德国人用一个点“．”来表示平方根，两点“．．”表示4次方根，三个点“．．．”表示立方根，比如，．3、．．3、．．．3就分别表示3的平方根、4次方根、立方根。

到十六世纪初，可能是书写快的缘故，小点上带了一条细长的尾巴，变成“√￣”。

1525年，路多尔夫在他的代数著作中，首先采用了“√”作为根号，比如他写√4是2，√9是3，但是这种写法未得到普遍的认可与采纳。

十七世纪，法国数学家笛卡尔（1596-1650年）第一个使用了现今用的根号“√￣”。

Tip:按住ALT，然后按顺序按41420（小键盘）就可以打出电脑中的根号“√￣”。

图1 学生展示与内容板书

2.  积分符号“∫”的诞生

莱布尼茨于1675年以“omn.l”表示l的总和（积分（Integrals）），而omn为omnia（意即所有、全部）之缩写。

后他又改写为∫，以“∫l”表示所有l的总和（Summa）。∫为字母s的拉长。

于1694年至1695年之间，将∫号后置一逗号，如 ∫,f(x)dx。

1698年，约翰·伯努利把逗号去掉，后更发展为现今之用法。
傅立叶是最先采用定积分符号（Signs for Definite Integrals）的人。

3.  常用的几何符号

常见的几何符号

任何一种符号的普遍采用都是非常艰难，它是人们在悠久的岁月中，经过不断改良、选择和淘汰的结果，它是数学家们集体智慧的结晶，而不是某一个人凭空臆造出来的，也绝不是从天上掉下来的

 

图2 师生认真学习

第二篇：数学符号发音

4.  24个希腊字母及其读音

希腊字母（英文：Greek alphabet，希腊文：Ελληνικό αλφάβητο）是希腊语所使用的字母，也广泛使用于数学、物理、生物、化学、天文等学科。希腊字母与拉丁字母、西里尔字母类似，为全音素文字。希腊字母是世界上最早拥有表示元音音位的字母的书写系统。俄语、乌克兰语等使用的西里尔字母和格鲁吉亚语字母都是由希腊字母发展而来。希腊语中一些与希腊字母有关的词汇进入到了许多语言，如Delta（三角洲）这个词汇就来自希腊字母Δ，因为Δ的形状是三角形

 

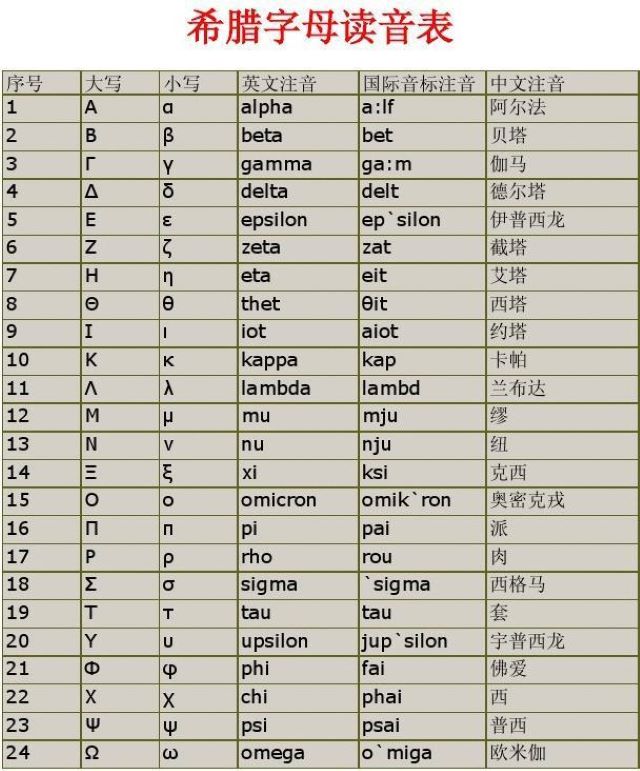
希腊字母读音表

本次形式丰富、交流畅达的课堂活动，不止提高了学生的获得感，也加深了我对博雅教育的认识。博雅教育实施的教学法，不是单纯的教授知识而是提倡互动，鼓励学生质疑种种假设和结论，在思维的激烈碰撞中互相学习，以使学习过程实现民主化。我们远景学院始终奉行：“每一堂课，就是一次学生的生命运动”，只要学生足够投入，通过师生之间有温度的讨论，就可以训练自己的公众表达与批判思维能力。

图3 小组合影留念